Molte volte, nella trattazione di mezzi trasmissivi o in genereale di circuiti elettronici, si cerca di capire come un segnale (di tensione o di corrente) applicato all’ingresso di un dispositivo ne esca “cambiato”. Ciò è conseguenza sia del segnale stesso e sia del mezzo attraversato. Si ragiona allora in termini di “frequenza”. Nozioni legate alla banda passante, o in generale alla “funzione di trasferimento”, permettono di capire come il segnale di uscita sia stato modificato durante il passaggio in tale mezzo.
Concetti come Integrale , Numeri Complessi, Serie di Fourier, Trasformata di Fourier, Trasformata di Laplace, sono le basi di una tale trattazione.
Per tale argomento, si cita come fonte il testo “TEORIA DEI SEGNALI – Prof. Paolo Mandarini – Casa editrice EUROMA”
Vista la complessità di tale argomento, è stato suddivisa tale trattazione in 6 articoli. Alcuni concetti non verranno spiegati ma solo menzionati mentre per i teoremi verrà dato solo l’enuciato visto che le dimostrazioni risultano essere molto lunghe.
Iniziamo con il caso di Segnali Periodici con periodo T (ossia segnali che presentano una ripetizione della loro forma d’0nda : x(t)=x(t +T) )
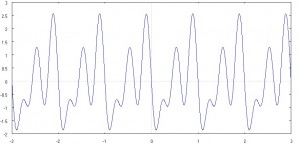 |
Considerare x(t) periodico di periodo T significa dire che il valore di x(t) assunto nel punto -T/2 sarà sicuramente uguale al valore di x(t) assunto nel punto T/2.
In tale situazione si definisce Frequenza Fondamentale del segnale periodico, l’inverso del periodo T : F=1/T
Ora se x(t) è periodico e se nell’intervallo da -T/2 a T/2 tale x(t) è assolutamente integrabile, allora x(t) si può esprimere tramite lo sviluppo in Serie di Fourier:
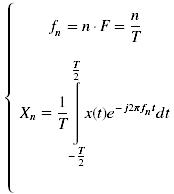 |
dove l’esponenziale complesso ( detto anche Funzione Elementare Complessa o Armonica di Ordine n )all’interno della sommatoria corrisponde a
ossia ad una funzione con valori complessi.
In definitiva si ha che ogni segnale periodico può essere visto come la somma di una infinità numerabile (n è un valore intero che va da – ∞ a + ∞) di segnali elementari del tipo
Ciascuno dei segnali elementari viene detto Componente Armonica a frequenza fn.
Per quanto riguarda il coefficiente Xn, esso risulta essere in genere complesso
 |
Questi coefficienti (si parla al plurare proprio per la presenza dell’indice n) possono essere rappresentati tramite una successione:
Tale successione prende il nome di Spettro di Ampiezza Complessa del segnale x(t)
Considerando x(t) reale (ossia che la funzione assuma solo valori reali) e visto che in questi articoli si considereranno tali, si ottiene un ulteriore proprità:
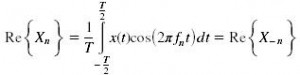 |
 |
ossia
Ora, poiché il Xn è complesso, esso puo essere rappresentato tramite modulo e fase:
In questo caso, le successioni dei moduli e delle fasi
vengono chiamati Spettro di Modulo e Spettro di Fase del segnale. Avendo considerato x(t) reale, anche per tali successioni vale la proprità:
Vediamo un caso in cui applicare tale trasfomazione.
Consideriamo il seguente segnale:
 |
Lo Spettro di Ampiezza Complessa assume i seguenti valori:
| Re{Xn} |
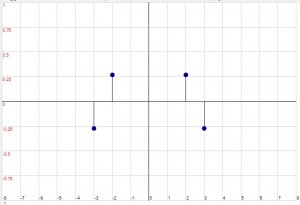 |
| Im{Xn} |
 |
Lo Spettro di Modulo risulta essere
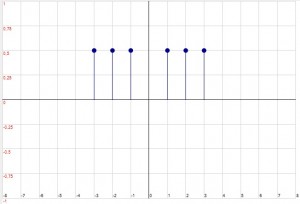 |
mentre lo Spettro di Fase
 |
In definitiva le armoniche di ordine 1, 2,3, -1,-2 e -3 contribuisco alla rappresentazione del segnale.
Per quanto riguada la Potenza Totale di un segnale, può essere espressa nel caso di un segnale periodico per mezzo dello spettro di x(t):
 |
In tale case, la successione dei contributi delle potenze totali dei singoli segnali elementari rappresenta lo SPETTRO DI POTENZA del segnale x(t)
Per l’esempio precedentemente considerato, lo Spettro di Potenza risulta essere
 |
Ora il coefficiente Xn dipende da n. Ma in realtà si può dire che Xn sia funzione della frequenza, ed in particolare in funzione delle f per cui :
Allora si può dire che la successione dei coefficienti Xn, puo essere rappresenta da un unica funzione :
che prende il nome di Inviluppo dello Spettro di Ampiezza. Allora x(t) può essere espressa come
In questo caso, alla precedente rappresentazione si da il nome di Rappresentazione Nel Dominio Della Frequenza del segnale x(t).